八字模型是几何中的一个常见模型,通常指由两条相交直线形成的两个三角形组成的图形,形状类似汉字“八”。其核心结论如下:
八字模型的核心结论
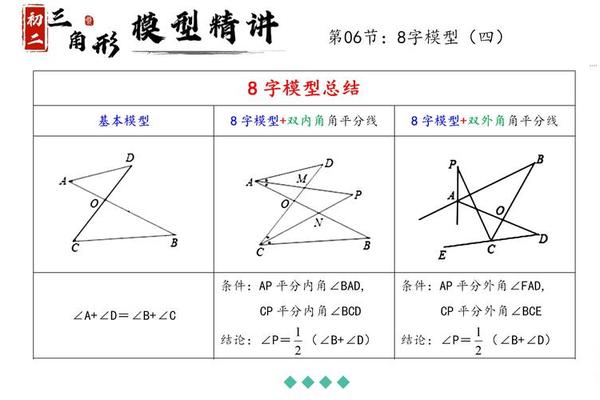
在八字模型中,若两个三角形有一对对顶角,则这两个三角形的其他两个内角之和相等。
具体表述:
设两直线相交于点 ( O ),形成三角形 (
riangle OAB ) 和 (
riangle OCD ),其中 ( angle AOB ) 和 ( angle COD ) 为对顶角(相等),则:
[
angle OAB + angle OBA = angle OCD + angle ODC
]
证明
1. 三角形内角和定理:
在 (
riangle OAB ) 中,有:
[
angle OAB + angle OBA + angle AOB = 180^circ
]
同理,在 (
riangle OCD ) 中:
[
angle OCD + angle ODC + angle COD = 180^circ
]
2. 对顶角相等:
[
angle AOB = angle COD
]
3. 联立方程:

由上述两式可得:
[
angle OAB + angle OBA = 180^circ
]
[
angle OCD + angle ODC = 180^circ
]
因此:
[
angle OAB + angle OBA = angle OCD + angle ODC
]
应用场景
1. 角度关系推导:
在复杂几何问题中,利用八字模型可快速得出某些角的和或差的关系,简化计算。
2. 相似三角形判定:
若进一步满足其他条件(如对应边成比例或另一对角相等),可推导出三角形相似,进而解决比例问题。
示例
如图,已知 ( angle AOB = angle COD = 50^circ ),且 ( angle OAB = 30^circ ),求 ( angle OCD + angle ODC )。
解:
根据八字模型结论:
[
angle OAB + angle OBA = angle OCD + angle ODC
]
已知 ( angle OAB = 30^circ ),则:
[
30^circ + angle OBA = 180^circ
]
因此:
[
angle OCD + angle ODC = 30^circ + 100^circ = 130^circ
]
该结论是八字模型的基础,适用于解决涉及对顶角及角度和的几何问题。在更复杂的情况下,可结合相似三角形或平行线性质进一步拓展应用。


